Unlock Gradient Descent: 3D Visualization, be the best

Gradient Descent is one of the most fundamental concepts in machine learning and optimization. But understanding it can be more intuitive when we visualize the trajectory of a function’s optimization process. In this blog, we’ll break down a Python script that demonstrates gradient descent in a 3D landscape and explain each section step-by-step. By the end, you’ll have a clearer understanding of the optimization process and how to bring it to life using Python.

The Mathematics Behind Gradient Descent

Before diving into the code implementation, let’s break down the mathematics that powers Gradient Descent. At its core, Gradient Descent is an iterative optimization algorithm that minimizes a function f(x,y)f(x, y)f(x,y) by following the steepest descent path.

Step 1: Gradient of the Function

The gradient of a function f(x,y)f(x, y)f(x,y) is a vector of partial derivatives:

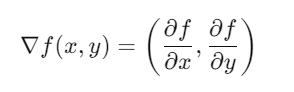
Each component of the gradient indicates the rate of change of f(x,y)f(x, y)f(x,y) with respect to xxx and yyy.
In our function:

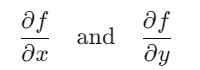
are calculated using symbolic differentiation (sympy.diff).

Step 2: Gradient Descent Update Rule

Gradient Descent updates the current position (x,y)(x, y)(x,y) iteratively using:

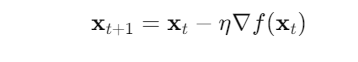
Gradient Descent

Where:

Step 3: Convergence

The algorithm stops when:

The gradient becomes nearly zero, indicating a local minimum.
A maximum number of iterations (epochs) is reached.

Example for Our Function

Let’s consider our function:

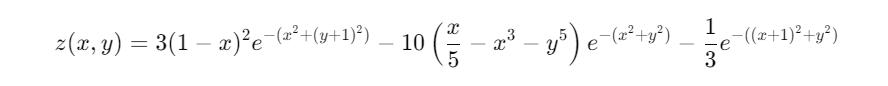
Gradients:

2. Update Rule:

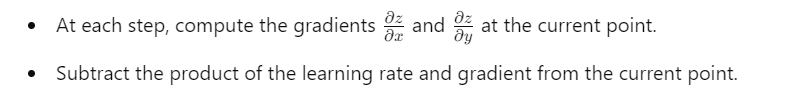
3. Visualization:

The algorithm moves the point closer to a local minimum by iteratively adjusting xxx and yyy based on the steepest descent.

This mathematical foundation ensures that the algorithm converges towards a local minimum, as visualized in the trajectory plot.

Importing Libraries

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import sympy as sp

Here’s what each library does:

numpy: Handles numerical operations efficiently.
matplotlib.pyplot: Used for 2D and 3D plotting.
mpl_toolkits.mplot3d: Enables 3D plotting in Matplotlib.
sympy: A symbolic mathematics library, perfect for working with derivatives.

Defining the Function and Its Gradients

x_sym, y_sym = sp.symbols('x y')
z_sym = 3*(1-x_sym)**2*sp.exp(-(x_sym**2) - (y_sym+1)**2) \
        - 10*(x_sym/5 - x_sym**3 - y_sym**5)*sp.exp(-x_sym**2 - y_sym**2) \
        - 1/3*sp.exp(-(x_sym+1)**2 - y_sym**2)
df_x = sp.lambdify((x_sym, y_sym), sp.diff(z_sym, x_sym))
df_y = sp.lambdify((x_sym, y_sym), sp.diff(z_sym, y_sym))

This section:

Defines the mathematical function (z_sym) to be optimized. The function is a mix of exponential and polynomial terms, creating a “bumpy” landscape ideal for visualization.
Computes the gradients (df_x and df_y) with respect to x and y using sympy.diff.
Converts symbolic expressions into Python functions using sympy.lambdify.

Setting Up Gradient Descent Parameters

np.random.seed(42)  # For reproducibility
localmin = np.random.rand(2)  # Random starting point in [-2, 2]
startpnt = localmin.copy()

learning_rate = 0.01
training_epoch = 1000

localmin initializes the starting point for optimization. learning_rate controls the step size in each iteration. training_epoch determines the number of optimization steps.

Performing Gradient Descent

trajectory = np.zeros((training_epoch, 2))
for i in range(training_epoch):
    grad_x = np.array([df_x(localmin[0], localmin[1]),
                       df_y(localmin[0], localmin[1])])
    localmin = localmin - learning_rate * grad_x
    trajectory[i, :] = localmin

trajectory keeps track of all points visited during the optimization.
In each iteration:

The gradients at the current point are calculated.
The point is updated by subtracting the gradient scaled by the learning rate.

The process continues for all epochs, creating a path towards a local minimum.

Generating Data for the Surface

x = np.linspace(-3, 3, 201)
y = np.linspace(-3, 3, 201)
X, Y = np.meshgrid(x, y)
Z = peaks(x, y)

This step creates a grid of points (X, Y) and evaluates the function values (Z) at those points to plot the 3D surface.

Visualizing the Optimization Path

fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection='3d')

ax.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8, edgecolor='none')

traj_z = ...
ax.plot(trajectory[:, 0], trajectory[:, 1], traj_z, color='r', marker='o', markersize=3, label='Gradient Descent Trajectory')

ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
ax.set_zlabel('Z-axis')
ax.set_title('3D Trajectory of Gradient Descent')
ax.legend()

plt.show()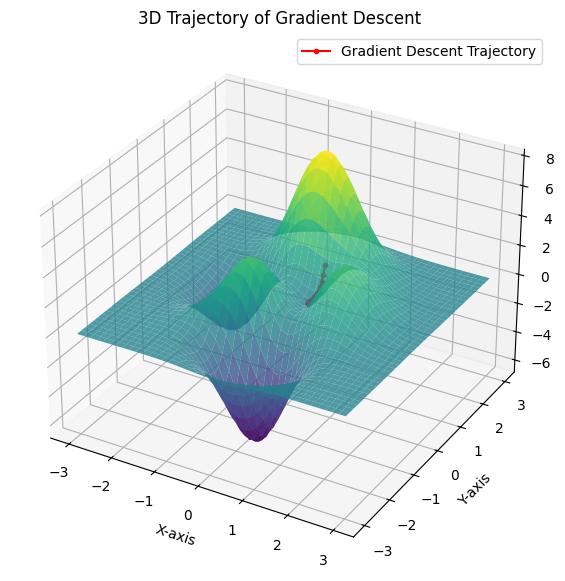

The surface plot visualizes the landscape of the function.
The trajectory plot overlays the gradient descent path, showing how it moves towards the minimum.

Key Insights

Gradient descent’s effectiveness depends on parameters like learning rate:
- Too high, and it overshoots the minimum.
- Too low, and it converges too slowly.
Initial starting points matter:
- In non-convex functions like this, different starting points may lead to different local minima.
Visualization provides intuition:
- Seeing the trajectory helps understand optimization dynamics better.

Interactive 3D graph

import numpy as np
import plotly.graph_objects as go
import sympy as sp

# Define the function and its derivatives
x_sym, y_sym = sp.symbols('x y')
z_sym = 3*(1-x_sym)**2*sp.exp(-(x_sym**2) - (y_sym+1)**2) \
        - 10*(x_sym/5 - x_sym**3 - y_sym**5)*sp.exp(-x_sym**2 - y_sym**2) \
        - 1/3*sp.exp(-(x_sym+1)**2 - y_sym**2)
df_x = sp.lambdify((x_sym, y_sym), sp.diff(z_sym, x_sym))
df_y = sp.lambdify((x_sym, y_sym), sp.diff(z_sym, y_sym))


localmin = np.random.rand(2)  # Random starting point in [-2, 2]
startpnt = localmin.copy()

learning_rate = 0.01
training_epoch = 1000  # Reduced for visualization purposes

# Track trajectory
trajectory = np.zeros((training_epoch, 2))
for i in range(training_epoch):
    grad_x = np.array([df_x(localmin[0], localmin[1]),
                       df_y(localmin[0], localmin[1])])
    localmin = localmin - learning_rate * grad_x
    trajectory[i, :] = localmin

# Generate data for the surface
x = np.linspace(-6, 8, 201)
y = np.linspace(-6, 8, 201)
X, Y = np.meshgrid(x, y)
Z = 3*(1-X)**2*np.exp(-(X**2) - (Y+1)**2) \
    - 10*(X/5 - X**3 - Y**5)*np.exp(-X**2 - Y**2) \
    - 1/3*np.exp(-(X+1)**2 - Y**2)

# Compute Z values for the trajectory
traj_z = 3*(1-trajectory[:, 0])**2*np.exp(-(trajectory[:, 0]**2) - (trajectory[:, 1]+1)**2) \
         - 10*(trajectory[:, 0]/5 - trajectory[:, 0]**3 - trajectory[:, 1]**5)*np.exp(-trajectory[:, 0]**2 - trajectory[:, 1]**2) \
         - 1/3*np.exp(-(trajectory[:, 0]+1)**2 - trajectory[:, 1]**2)

# Create a Plotly 3D surface
surface = go.Surface(z=Z, x=x, y=y, colorscale='Viridis', opacity=0.8)
trajectory_line = go.Scatter3d(
    x=trajectory[:, 0],
    y=trajectory[:, 1],
    z=traj_z,
    mode='lines+markers',
    marker=dict(size=4, color='red'),
    line=dict(color='red', width=2),
    name='Gradient Descent Trajectory'
)

# Combine plots
fig = go.Figure(data=[surface, trajectory_line])
fig.update_layout(
    scene=dict(
        xaxis_title='X-axis',
        yaxis_title='Y-axis',
        zaxis_title='Z-axis'
    ),
    title='Interactive 3D Trajectory of Gradient Descent',
)

fig.show()

Now it’s your turn! Implement the code, tweak the parameters, and see how the path changes. Happy coding! 🚀

Amarnath Pandey